SChand CLASS 10 Chapter 5 Quadratic Equations Exercise 5E

Exercise 5D

---

Q1 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 1

The sum of the squares of two consecutive positive even integers is 100. Find the integers.

Sol :

Let two consecutive positive even integers are x and (x + 2). Then, we have

$x^2 + (x + 2)^2 = 100$

⇒ $x^2 + x^2 + 4x + 4 = 100$

⇒ $2x^2 + 4x – 96 = 0 $

⇒ $x^2 + 2x – 48 = 0 $

⇒ $x^2 + 8x – 6x – 48 = 0$

⇒ x(x + 8) – 6(x + 8) = 0

⇒ (x – 6)(x + 8) = 0

⇒ x = 6 or -8

Since x is positive even integer, then x = 6 and hence other positive even integer is (x + 2) = 8.

Thus, the required integers are 6 and 8.

---

Q2 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 2

Find two rational numbers which differ by 3 and the sum of whose squares is 117.

Sol :

Let two rational numbers are x and (x + 3). Then, we have

$x^2 + (x + 3)^2 = 117$

⇒ $x^2 + x^2 + 6x + 9 = 117$

⇒ $2x^2 + 6x + 9 = 117$

⇒ $2x^2 + 6x – 108 = 0$

⇒ $x^2 + 3x – 54 = 0$

⇒ $x^2 + 9x – 6x – 54 = 0$

⇒ x(x + 9) – 6(x + 9) = 0

⇒ (x – 6)(x + 9) = 0

⇒ x = 6 or -9

If x = 6, then (x + 3) = 9

If x = -9, then (x + 3) = -6

Thus, the required rational numbers are 6 and 9 or -9 and -6.

---

Q3 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 3

What number increased by its reciprocal equals $\frac{65}{8}$?

Sol :

Let the number is x. Then, we have

$x + \frac{1}{x} =\frac{65}{8}$

⇒ $\frac{(x^2 + 1)}{x} =\frac{65}{8}$

⇒ $8(x^2 + 1) = 65x$

⇒ $8x^2 – 65x + 8 = 0$

⇒ $8x^2 – 64x – x + 8 = 0$

⇒ 8x(x – 8) – 1(x – 8) = 0

⇒ (8x – 1)(x – 8) = 0

⇒ $x = \frac{1}{8}$ or 8

Thus, the required number is 8 or $\frac{1}{8}$.

---

Q4 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 4

The sum of the numerator and denominator of a certain fraction is 8. If 2 is added to the numerator and to the denominator, the value of the fraction is increased by 4/35. Find the fraction.

Sol :

Let the fraction is $\frac{x }{(8 – x)}$.

Then, we have

⇒ $\frac{(x + 2)}{(8 – x + 2)} = \frac{x}{(8 – x) }+ \frac{4}{35}$

⇒ $\frac{(x + 2)}{(10 – x) }– \frac{x}{(8 – x) }= \frac{4}{35}$

⇒ $ [(x + 2)(8 – x) – \frac{x(10 – x)]}{(10 – x)(8 – x) }= \frac{4}{35}$

⇒ $\frac{[8x – x^2 + 16 – 2x – 10x + x^2]}{(80 – 10x – 8x + x^2) }=\frac{4}{35}$

⇒ $35[16 – 4x] = 4(x^2 – 18x + 80)$

⇒ $35[4 – x] = (x^2 – 18x + 80)$

⇒ $x^2 + 17x – 60 = 0$

⇒ $x^2 + 20x – 3x – 60 = 0$

⇒ x(x + 20) – 3(x + 20) = 0

⇒ (x – 3)(x + 20) = 0

⇒ x = 3 or -20

Thus, the required fraction is $\frac{x}{(8 – x)}=\frac{ 3}{5}$

---

Q5 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 5

There are three consecutive integers such that the square of the first increased by the product of the other two gives 154. Find the integers.

Sol :

Let three consecutive integers are x, (x + 1) and (x + 2). Then, we have

⇒ $x^2 + (x + 1)(x + 2) = 154$

⇒ $x^2 + x2 + 3x + 2 = 154$

⇒ $2x^2 + 3x – 152 = 0$

⇒ $2x^2 – 16x + 19x – 152 = 0$

⇒ 2x(x – 8) + 19(x – 8) = 0

⇒ (2x + 19)(x – 8) = 0

⇒ $x = \frac{-19}{2}$ or 8.

Thus, the required three consecutive integers are 8, 9, 10.

---

Q6 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 6

The sum of two numbers is 8 and 15 times the sum of their reciprocals is also 8. Find the numbers.

Sol :

Let two numbers are x and (8 – x). Then, we have

⇒ $15\left[\frac{1}{x}+ \frac{1}{(8 – x)}\right] = 8$

⇒ $\frac{15(8 – x + x)}{x(8 – x)} = 8$

⇒ 15(8) = 8x(8 – x)

⇒ 15 = x(8 – x)

⇒ $x^2 – 8x + 15 = 0$

⇒ $x^2 – 3x – 5x + 15 = 0$

⇒ x(x – 3) – 5(x – 3) = 0

⇒ (x – 5)(x – 3) = 0

⇒ x = 3 or 5

If x = 3, then (8 – x) = 5

If x = 5, then (8 – x) = 3

Thus, the required numbers are 3 and 5.

---

Q7 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 7

A two digit number is such that the product of the digits is 12. When 36 is added to this number, the digits interchange their places. Find the number.

Sol :

Let the unit digit of the number is x, then its tens digit is $\frac{12}{x}$.

Then, we have

⇒ $10\left(\frac{12}{x}\right) + x + 36 = 10x + \frac{12}{x}$

⇒ 9x – 9\left(\frac{12}{x}\right) = 36

⇒ $x –\left(\frac{12}{x}\right) = 4$

⇒ $\frac{(x^2 – 12)}{x}= 4$

⇒ $(x^2 – 12) = 4x$

⇒ $x^2 – 4x – 12 = 0$

⇒ $x^2 – 6x + 2x – 12 = 0$

⇒ x(x – 6) + 2(x – 6) = 0

⇒ (x + 2)(x – 6) = 0

⇒ x = -2 or 6

Since x is a digit, then x = 6.

Thus, the unit digit is x = 6 and tens digit $\frac{12}{x}= 2$ and hence the number is 26

---

Q8 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 8

Five times a certain whole number is equal to three less than twice the square of the number. Find the number.

Sol :

Let the whole number is x. Then, we have

⇒ $5x = 2x^2 – 3$

⇒ $2x^2 – 5x – 3 = 0$

⇒ $2x^2 – 6x + x – 3 = 0$

⇒ 2x(x – 3) + 1(x – 3) = 0

⇒ (2x + 1)(x – 3) = 0

⇒ $x = \frac{-1}{2}$ or 3

Since x is a whole number, then the required number is x = 3.

---

Q9 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 9

Three consecutive numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Assume the middle number to be x and form a quadratic equation satisfying the above statement. Hence, find the three numbers.

Sol :

Let the three number are (x – 1), x, (x + 1).

Then, we have

⇒ $x^2 = (x + 1)^2 – (x – 1)^2 + 60$

⇒ $x^2 = x^2 + 2x + 1 – x^2 + 2x – 1 + 60$

⇒ $x^2 – 4x – 60 = 0$

⇒ $x^2 – 10x + 6x – 60 = 0$

⇒ x(x – 10) + 6(x – 10) = 0

⇒ (x + 6)(x – 10) = 0

⇒ x = -6 or 10

Thus, the three numbers are 9, 10 and 11.

---

Q10 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 10

The sum of the ages (in years) of a son and his father is 35 and the product of their ages is 150. Find their ages.

Sol :

Let the father’s age is x years then his son’s age is (35 – x) years. Then, we have

⇒ x(35 – x) = 150

⇒ $35x – x^2 = 150$

⇒ $x^2 – 35x + 150 = 0$

⇒ $x^2 – 30x – 5x + 150 = 0 $

⇒ x(x – 30) – 5(x – 30) = 0

⇒ (x – 5)(x – 30) = 0

⇒ x = 5 or 30

Thus, the father’s age is x = 30 years then his son’s age is (35 – x) = 5 years

---

Q11 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 11

Anjali was born in 1985 A.D. In the year $x^2$ AD, she was (x – 5) years old. Find the value of x.

Sol :

In the year $x^2$ AD, Anjali was (x – 5) years old. Then, we have

$x^2 – 1985 = (x – 5)$

⇒ $x^2 – x – 1980 = 0$

⇒ $x^2 – 45x + 44x – 1980 = 0$

⇒ x(x – 45) + 44(x – 45) = 0

⇒ (x + 44)(x – 45) = 0

⇒ x = -44 or 45

Since x is year, x = 45.

---

Q12 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 12

The difference of mother’s age and her daughter’s age is 21 years and the twelfth part of the product of their ages is less than the mother’s age by 18 years. Find their ages.

Sol :

Let the daughter’s age is x years then her mother’s age is (x + 21) years. Then, we have

⇒ $\frac{x(x + 21) }{ 12 }= (x + 21) – 18$

⇒ $x^2 + 21x = 12(x + 3)$

⇒ $x^2 + 21x = 12x + 36$

⇒ $x^2 + 9x – 36 = 0$

⇒ $x^2 + 12x – 3x – 36 = 0$

⇒ (x + 12) – 3(x + 12) = 0

⇒ (x – 3)(x + 12) = 0

⇒ x = 3 or -12

Since x is an age, x = 3

Thus, daughter’s age is x = 3 years and mother’s age is (x + 21) = 24 years.

---

Q13 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 13

Reena is x year old, while her father Mr. Sunil is $x^2$ years old. 5 years hence, Mr Sunil will be three times as old as Reena. Find their present ages.

Sol :

Given that Reena is x year old, while her father Mr. Sunil is x2 years old.

After 5 years, Mr Sunil will be three times as old as Reena.

Then, we have

⇒ $x^2 + 5 = 3(x + 5)$

⇒ $x^2 – 3x – 10 = 0$

⇒ $x^2 – 5x + 2x – 10 = 0$

⇒ x(x – 5) + 2(x – 5) = 0

⇒ (x + 2)(x – 5) = 0

⇒ x = -2 or 5

Since x is an age, x = 5.

Thus, Reena is x = 5 year old and her father Mr. Sunil is $x^2$ = 25 years old.

---

Q14 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 14

Form a quadratic equation from the following information, taking as width x ∈ N.

(i) The area of rectangle whose length is five more than twice its width is 75.

(ii) Solve the equation and find its length.

Sol :

Given that the width of rectangle is x, and hence the length of the rectangle is (2x + 5).

Then, we have

x(2x + 5) = 75

⇒ $2x^2 + 5x – 75 = 0$ [This is required quadratic equation.]

⇒ $2x^2 + 15x – 10x – 75 = 0$

⇒ x(2x + 15) – 5(2x + 15) = 0

⇒ (x – 5)(2x + 15) = 0

⇒ x = 5 or $\frac{-15}{2}$

Thus, the width of the rectangle is x = 5.

---

Q15 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 15

The sides of a right angled triangle containing the right angle are 5x cm and (3x – 1) cm. If the area of the triangle be $60 cm^2$, calculate the lengths of the sides of triangle.

Sol :

Given that the area of a right angled triangle, whose legs are 5x cm and (3x – 1) cm, is 60 cm2.

Then, we have

⇒ $\left(\frac{1}{2}\right) × (5x) × (3x – 1) = 60$

⇒ $15x^2 – 5x – 120 = 0$

⇒ $5(3x^2 – x – 24) = 0$

⇒ $3x^2 – x – 24 = 0$

⇒ $3x^2 – 9x + 8x – 24 = 0$

⇒ 3x(x – 3) + 8(x – 3) = 0

⇒ (3x + 8)(x – 3) = 0

⇒ x = 3 or $\frac{-8}{3}$

Thus, the legs of the right angled triangle are 5x = 15 and (3x – 1) = 8 and hence its hypotenuse is √(82 + 152) = 17.

---

Q16 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 16

The hypotenuse of a right angle triangle is 13 cm and the difference between the other two sides is 7 cm.

(i) Taking x as the length of the shorter of the two sides, write an equation in x that represents the above statement.

(ii) Solve the equation obtained in (i) above and hence find the two unknowns sides of the triangle.

Sol :

Let the length of legs of right angled triangle are x and (x + 7). Then, we have

⇒ $x^2 + (x + 7)^2 = 13^2$

⇒ $x^2 + x^2 + 14x + 49 = 169$

⇒ $2x^2 + 14x – 120 = 0$

⇒ $x^2 + 7x – 60 = 0$ [This is required quadratic equation.]

⇒ $x^2 + 12x – 5x – 60 = 0$

⇒ x(x + 12) – 5(x + 12) = 0

⇒ (x – 5)(x + 12) = 0

⇒ x = 5 or -12

Thus, the two legs of the right angled triangle are x = 5 and (x + 7) = 12.

---

Q17 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 17

The length of a verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.

(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement.

(ii) Solve the equation in (i) above and hence find the dimension of the verandah.

Sol :

Let the dimension of the verandah are x and (x + 3). Then, we have

x(x + 3) = 2(x + x + 3)

⇒ $x^2 + 3x = 4x + 6$

⇒ $x^2 – x – 6 = 0$ [This is required quadratic equation.]

⇒ $x^2 – 3x + 2x – 6 = 0$

⇒ x(x – 3) + 2(x – 3) = 0

⇒ (x + 2)(x – 3) = 0

⇒ x = 3 or -2.

Thus, the dimension of the verandah are width as x = 3 and length as (x + 3) = 6.

---

Q18 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 18

Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 sq cm. Express this as an algebraic equation in x and solve the equation to find sides of the squares.

Sol :

Two squares have sides x cm and (x + 4) cm. Then, we have

⇒ $x^2 + (x + 4)^2 = 656$

⇒ $x^2 + x^2 + 8x + 16 = 656$

⇒ $2x^2 + 8x – 640 = 0$

⇒ $x^2 + 4x – 320 = 0$ [This is required quadratic equation.]

⇒ $x^2 – 16x + 20x – 320 = 0$

⇒ x(x – 16) + 20(x – 16) = 0

⇒ (x + 20)(x – 16) = 0

⇒ x = -20 or 16

Since x represents the length of the side of square, then x = 16.

Thus, the sides of the squares are 16 cm and 20 cm.

---

Q19 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 19

The perimeter of a rectangular plot is 180 m and its area is 1800 cm2. Take the length of plot as x m. Use the perimeter 180 m to write the value of the breadth in terms of x. Use the values of length, breadth and the area to write an equation in x. Solve the equation to calculate the length and breadth of the plot.

Sol :

Given that the length of rectangular plot is x m. Then, we have

2(length + breadth) = 180

⇒ 2(x + breadth) = 180

⇒ breadth = 90 – x.

Now, Area = 1800

⇒ x(90 – x) = 1800

⇒ $90x – x^2 = 1800$

⇒ $x^2 – 90x + 1800 = 0$

⇒ $x^2 – 60x – 30x + 1800 = 0$

⇒ x(x – 60) – 30(x – 60) = 0

⇒ (x – 30)(x – 60) = 0

⇒ x = 30 or 60.

If x = 30, then 90 – x = 60

If x = 60, then 90 – x = 30

Thus, length = 60 cm and width = 30 cm

---

Q20 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 20

A rectangle has an area of $24 cm^2$. If its length is x cm, write down its breadth in terms of x. Given that its perimeter is 20 cm, form an equation in x and solve it.

Sol :

Given that the length of rectangle is x m. Then, we have

length * breadth = 24

⇒ x * breadth = 24

⇒ breadth $= \frac{24}{x}$.

Now, Perimeter = 20

⇒ $2\left(x + \frac{24}{x}\right) = 20$

⇒ $\left(x + \frac{24}{x}\right) = 10$

⇒ $x^2 + 24 = 10x$

⇒ $x^2 – 10x + 24 = 0$

⇒ $x^2 – 6x – 4x + 24 = 0$

⇒ x(x – 6) – 4(x – 6) = 0

⇒ (x – 4)(x – 6) = 0

⇒ x = 4 or 6

Since x is length of the rectangle, then x = 6 and $\frac{24}{x}= 4$

Thus, length and breadth of the rectangle are 6 cm and 4 cm.

---

Q21 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 21

A rectangular garden 10 m by 16 m is to be surrounded by a concrete path of uniform width. Given that the area of the path is 120 squares meters, assuming the width of the path to be x, form an equation in x and solve it to find the value of x.

Sol :

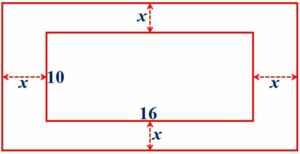
Given that the width of the wall to be x. Then, we have

(2x + 16)(2x + 10) – 10 × 16 = 120

⇒ $4x^2 + 52x + 160 – 160 = 120$

⇒ $4x^2 + 52x – 120 = 0$

⇒ $x^2 + 13x – 30 = 0$

⇒ $x^2 + 15x – 2x – 30 = 0$

⇒ x(x + 15) – 2(x + 15) = 0

⇒ (x – 2)(x + 15) = 0

⇒ x = 2 or -15

Thus, the width of the path is x = 2 cm.

---

Q22 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 22

A man covers a distance of 200 km travelling with a uniform speed of x km per hour. The distance could have been covered in 2 hours less, had the speed been (x + 5)km/hr. Calculate the value of x.

Sol :

According to question, we have

⇒ $\frac{200}{x} – \frac{200}{(x + 5) }= 2$

⇒ $\frac{1}{x}– \frac{1}{(x + 5)} =\frac{1}{100}$

⇒ $\frac{(x + 5 – x)}{x(x + 5)}= \frac{1}{100}$

⇒ $\frac{5}{x(x + 5)}= \frac{1}{100}$

⇒ $x^2 + 5x – 500 = 0$

⇒ $x^2 + 25x – 20x – 500 = 0$

⇒ x(x + 25) – 20(x + 25) = 0

⇒ (x – 20)(x + 25) = 0

⇒ x = 20 or -25.

Thus, required speed is x = 20 km/hr.

---

Q23 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 23

An express train makes a run of 240 km at a certain speed. Another train, whose speed is 12 km/hr less than the first takes an hour longer to make the same trip. Find the speed of the express train to km/hr.

Sol :

Let the speed of the express train is x km/hr, we have

⇒ $\frac{240}{(x – 12)} –\frac{240}{x}= 1$

⇒ $\frac{1}{(x – 12)} –\frac{ 1}{x }= \frac{1}{240}$

⇒ $\frac{(x – x + 12)}{x(x – 12)} =\frac{ 1}{240}$

⇒ $\frac{12}{x(x – 12)} = \frac{1}{240}$

⇒ $x^2 – 12x – 2880 = 0$

⇒ $x^2 – 60x + 48x – 2880 = 0$

⇒ x(x – 60) + 48(x – 60) = 0

⇒ (x + 48)(x – 60) = 0

⇒ x = -48 or 60

Thus, the speed of the express train is 60 km/hr.

---

Q24 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 24

A train covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hr more, it would have taken 30 minutes less for the journey. Find the original speed of the train.

Sol :

Let the original speed of the train is x km/hr, we have

⇒ $\frac{90}{x}– \frac{90}}{(x + 15)} = \frac{1}{2}$

⇒ $\frac{1}{x} – \frac{1}{(x + 15)} = \frac{1}{180}$

⇒ $\frac{(x + 15 – x)}{x(x + 15) }= \frac{1}{180}$

⇒ $\frac{15}{x(x + 15) }=\frac{1}{180}$

⇒ $x^2 + 15x – 2700 = 0$

⇒ $x^2 + 60x – 45x – 2700 = 0$

⇒ x(x + 60) – 45(x + 60) = 0

⇒ (x – 45)(x + 60) = 0

⇒ x = 45 or -60

Thus, the original speed of the train is x = 45 km/hr.

---

Q25 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 25

A plane left 30 minutes later than the scheduled time and in order to reach its distance, 1500 km away it has to increase its speed by 250 km/hr from its usual speed. Find its usual speed.

Sol :

Let the usual speed of the plain is x km/hr, we have

⇒ $\frac{1500}{x} – \frac{1500}{(x + 250) }= \frac{1}{2}$

⇒ $\frac{1}{x}– \frac{1}{(x + 250)} = \frac{1}{3000}$

⇒ $\frac{(x + 250 – x)}{x(x + 250)} = \frac{1}{3000}$

⇒ $\frac{250}{x(x + 250)} = \frac{1}{3000}$

⇒ $x^2 + 250x – 750000 = 0$

⇒ $x^2 + 1000x – 750x – 750000 = 0$

⇒ x(x + 1000) – 750(x + 1000) = 0

⇒ (x – 750)(x + 1000) = 0

⇒ x = 750 or -1000.

Thus, the usual speed of the plain is 750 km/hr.

---

Q26 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 26

A boat takes 1 hour longer to go 36 km up a river than to return. If the river flows at 3 km/hr, find the rate at which the boat travels in still water.

Sol :

Let the speed of the boat in still water is x km/hr, we have

⇒ $\frac{36}{(x – 3) }– \frac{36}{(x + 3) }= 1$

⇒ $\frac{1}{(x – 3)} – \frac{1}{(x + 3)} =\frac{1}{36}$

⇒ $\frac{(x + 3 – x + 3)}{(x + 3)(x – 3)}= \frac{1}{36}$

⇒ $\frac{6}{(x + 3)(x – 3)} = \frac{1}{36}$

⇒ $\frac{1}{(x^2 – 9)}= \frac{1}{216}$

⇒ $x^2 = 225$

⇒ x = 15 or -15.

Thus, the speed of the boat in still water is x = 15 km/hr.

---

Q27 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question  27

A man purchased some horses for Rs. 3000. Three of them died, and he sold the rest at Rs. 65 more than what he paid for each horse and thus gained 6% more his outlay. How many horses did he buy?

Sol :

Let the number of horses purchased is x. Then, the price of each horse is Rs. 3000/x.

Now, CP = 3000 and SP $= 3000\left(1 + \frac{6}{100}\right)$ = 3180.

According to question, we have

⇒ $\frac{3180}{(x – 3)}= \frac{3000}{x} + 65$

⇒ $\frac{636}{(x – 3)} – \frac{600}{x} = 13$

⇒ 636x – 600x + 1800 = 13x(x – 3)

⇒ $36x + 1800 = 13x^2 – 39x$

⇒ $13x^2 – 75x – 1800 = 0$

⇒ $13x^2 – 195x + 120x – 1800 = 0$

⇒ 13x(x – 15) + 120(x – 15) = 0

⇒ (13x + 120)(x – 15) = 0

⇒ x = 15 or $\frac{-120}{13}$.

Thus, the number of horses purchased is x = 15.

---

Q28 | Ex-5E | Class 8 | S.Chand | Mathematics | Chapter 5 | Quadratic Equations | myhelper

OPEN IN YOUTUBE

Question 28

A trader bought a number of articles for Rs. 1200. Ten were damaged and he sold each of the rest at Rs. 2 more than what he paid for it, thus getting a profit of Rs. 60 on the whole transaction. Taking the number of article he bought as x, form an equation in x and solve.

Sol :

Let the number of article purchased is x. Then, the price of each article is Rs. $\frac{1200}{x}$.

Now, CP = 1200 and SP = 1200 + 60 = 1260.

According to question, we have

⇒ $\frac{1260}{(x – 10)}= \frac{1200}{x}+ 2$

⇒ $\frac{625}{(x – 10)} – \frac{600}{x} = 1$

⇒ $\frac{625}{(x – 10)} – \frac{600}{x}= 1$

⇒ 625x – 600x + 6000 = x(x – 10)

⇒ $x^2 – 40x – 6000 = 0$

⇒ $x^2 – 100x + 60x – 6000 = 0$

⇒ x(x – 100) + 60(x – 100) = 0

⇒ (x + 60)(x – 100) = 0

⇒ x = -60 or 100

Thus, the number of article purchased is x = 100.